Des probabilités avec 7 dés :
Rappel du problème :
- On lance un dé, le résultat obtenu est noté $x$.
- On lance $x$ dés, et on ajoute leurs résultats. On note $S$ cette somme.
Donner la loi de probabilité de $S$...
Vous avez le droit d'utiliser un tableur, mais c'est tout !
Solution :
Une image.
Il est un peu difficile de dessiner un arbre de probabilités complet représentant cette expérience aléatoire, mais il est assez facile d'en imaginer le début.
Voici un schéma montrant les différentes issues qui aboutissent à une somme égale à 3.

En notant $D$ la variable aléatoire égale au nombre de dés, la probabilité d'obtenir 3 est donc :
$$P(S=3)=\frac{1}{6} P_{D=1}(S=3)+\frac{1}{6} P_{D=2}(S=3)+\frac{1}{6} P_{D=3}(S=3)$$
Soit :
$$P(S=3)=\frac{1}{6^2} + 2 \times \frac{1}{6^3} + \frac{1}{6^4}$$
Le facteur 2 qui intervient dans le 2e terme de cette somme correspond au fait qu'il y a deux façons d'obtenir 3 avec 2 dés : 2+1 ou 1+2.
Nombre de façons d'obtenir $n$ avec $k$ dés.
Il faut donc étudier ce nombre...
On note $N(n,k)$ le nombre de façons d'obtenir une somme égale à $n$ avec $k$ dés. (Ce nombre vaut 1 si $n=2$ et $k=2$ et il vaut 2 si $n=3$ et $k=2$ par exemple ; il vaut 0 si $n>36$, si $k>6$ ou si $n$ ou $k<1$ ...)
Supposons qu'avec $k$ dés, la somme obtenue soit $n$, imaginons alors qu'on enlève le premier dé : le nombre de dés serait devenu $k-1$ et la somme $n-p$ où $p$ est le résultat du dé enlevé (entre 1 et 6).
On a donc :
$$N(n,k)=\sum_{p=1}^{6}N(n-p,k-1)$$
Cette formule permet de calculer rapidement (dans un tableur) les valeurs de $N(n,k)$ pour tous les $n$ et $k$ possibles :

Loi de probabilité.
Soit $n$ un entier entre 1 et 36. On a :
$$P(S=n)=\frac{1}{6} \sum_{k=1}^{6} P_{nbre de dés = k}(S=n)$$
$$P(S=n)=\frac{1}{6} \sum_{k=1}^{6} N(n,k)\frac{1}{6^k}$$
$$P(S=n)=\sum_{k=1}^{6} \frac{N(n,k)}{6^{k+1}}$$
On utilise encore le tableur et on obtient :
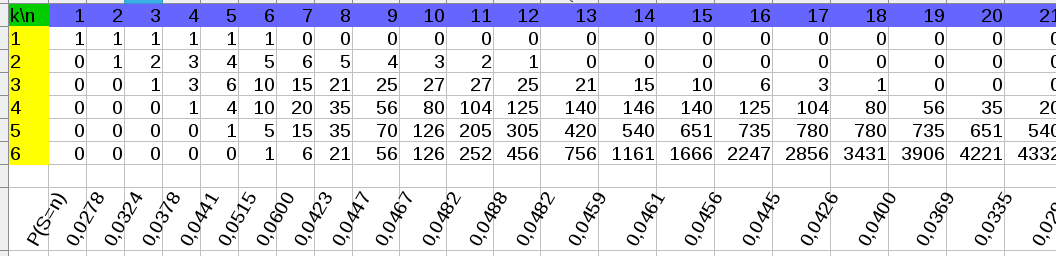
Pour mieux voir les choses, voici une représentation graphique de la loi de probabilité :
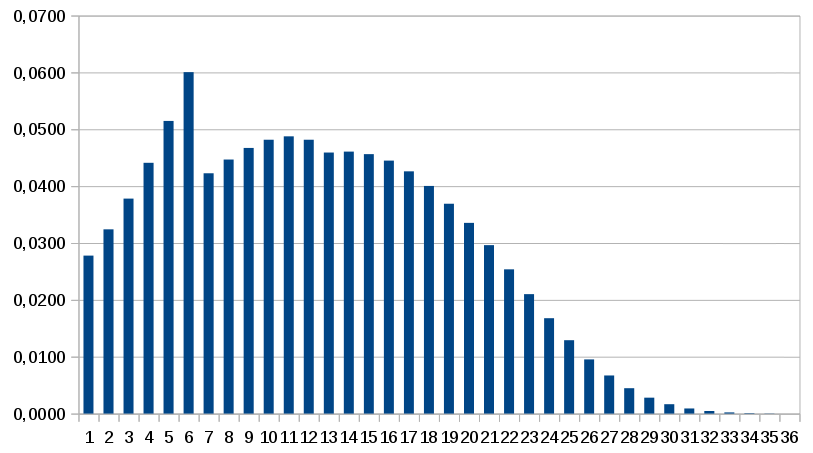
Marrant, n'est ce pas ?
Une petite remarque :
Lorsqu'on écrit : $3=1+2$, $3=2+1$ et $3=1+1+1$, on donne trois compositions du nombre 3. Ce qui est noté $N(n,k)$ ci-dessus est un dénombrement des compositions de $n$ en $k$ parties qui ne peuvent être supérieures à 6. Si on s'intéresse aux compositions de $n$ en $k$ parties, sans imposer de limite supérieure aux parties, il existe des formules simples.
Voir ici sur Wikipédia.
Cependant, il est difficile de donner une expérience aléatoire comme dans l'exemple étudié ici, où les dés n'auraient pas de limite supérieure à leur nombre de faces ! Si vous y arrivez, je veux bien lire votre idée !